RAZONES Y PROPORCIONES

 RAZONES:


Al realizar una encuesta entre los jóvenes entre 18 y 21 años se concluye que: "1 de cada 5 jóvenes está inscrito en el Registro Electoral". Entonces, se puede decir que la razón entre los que votan y el total de jóvenes es 1: 5. También se puede decir que la razón entre los que votan y los que no, es 1: 4.

Sean a y b dos números racionales y b ‡ 0, entonces una razón entre a y b es el cociente a: b = a/b y lo leeremos a es a b.

Como las razones son números racionales, entonces se puede ampliarla y simplificarla como se desee mientras se mantenga la razón. Raz Ej 1.JPG

Una de las situaciones matemáticas más frecuente es sin duda, la de relacionar dos cantidades: se han hecho al sumarlas y restarlas, o al multiplicarlas y dividirlas. En particular, al relacionarlas mediante la resta y la división, estamos comparándolas. Existen dos tipos de comparaciones entre números: las que nos permiten averiguar cuál es el mayor calculando la diferencia existente entre ambos, o bien, calculando cuántas veces el mayor contiene al menor. En la primera situación hablamos de comparaciones o relaciones aditivas y en la segunda, de relaciones multiplicativas.


EJEMPLO DE RAZONES:




PROPORCIONES:

La igualdad entre dos razones es una proporción.

Se lee:

  • a es a b como c es a d.
  • También puede escribirse a: b = c: d
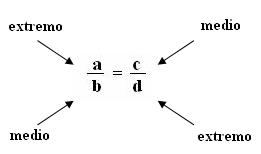
  • En toda proporción se tiene:

Terminos proporc.JPG

En toda proporción el producto de los extremos es igual al producto de los medios, esta relación se conoce como Teorema fundamental de la proporción, es decir.

Teorema propor.JPG

Un ejemplo de proporción es 2/3 = 4/6, cuya lectura es “2 es a 3 como 4 es a 6”. De nuevo hay que recordar la distinción entre razones y fracciones, para no ver en la expresión anterior “la equivalencia de dos fracciones” (que será la lectura correcta cuando se hable de fracciones, pero no ahora...).

Vamos con la nomenclatura relativa a las proporciones. El uso de la notación a : b : :c : d nos ayuda a identificar a los números a y d como los extremos de la proporción y a los números b y c como los medios de la proporción. Por ejemplo, en 2/3 = 4/6, 2 y 6 son los extremos de la proporción, y 3 y 4, los medios.


EJEMPLO DE PROPORCIONES:



AQUI TE DEJO UN VIDEO QUE TE PUEDE AYUDAR:



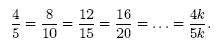
Comentarios

Publicar un comentario

Entradas más populares de este blog

MAGNITUDES DIRECTAMENTE PROPORCIONALES Y MAGNITUDES INVERSAMENTE PROPORCIONALES

Imagen
 MAGNITUDES DIRECTAMENTE PROPORCIONALES: Definición. Se dice que dos magnitudes son directamente proporcionales si al multiplicar o dividir una de ellas por un número, la otra queda multiplicada o dividida por el mismo número.              La razón o cociente entre la segunda y la primera magnitud, se llama constante de proporcionalidad directa.              Una forma de resolver actividades de magnitudes directamente proporcionales es mediante una regla de tres. Sin embargo este procedimiento se convierte en un método que se realiza de forma completamente mecánica, sin que se sepa realmente lo que se está haciendo.              Con esta primera escena se podrán resolver actividades de magnitudes directamente proporcionales de forma ordenada sin la utilización de números decimales. La escena indica los pasos a seguir para su resolución.                Una vez comprendido el procedimiento, con esta segunda escena se podrán resolver actividades de magnitudes directamente proporcionales c
Leer más

GARFICA DE FUNCION LINEAL

Imagen
 GRAFICA DE FUNCION LINEAL  Las gráficas de funciones lineales son  líneas rectas . Existen tres métodos básicos para graficar funciones lineales. El primero es graficar puntos y luego trazar una línea para unir los puntos. El segundo es usando el intercepto en y y la pendiente. ¿Cómo graficar una función lineal usando puntos? Paso 1:  Escoge un mínino de dos valores de entrada. Paso 2:  Evalúa la función en cada valor de entrada. Paso 3:  Usa los valores de salida resultantes para formar coordenadas cartesianas. Paso 4:  Grafica las coordenadas cartesianas en una cuadrícula. Paso 5:  Traza una línea a través de los puntos. Aqui hay un ejemplo que yo hice: Otro ejemplo: Grafica la función   usando puntos. Solución:  Empezamos escogiendo los valores de entradas. Vamos a escoger tres valores diferentes. Escogeremos el -2, 0 y 2. Evalúa la función en cada valor de entrada y usa el valor de salida para formar las coordenadas cartesianas de los puntos:         ⇒        ⇒        ⇒ Graficamos
Leer más